เอกสารนี้อธิบายความรู้เบื้องต้นเกี่ยวกับลักษณะการเคลื่อนที่ของอิเล็กตรอน ผ่านแม่เหล็กชนิดต่างๆ ที่เป็นส่วนประกอบหลักของวงกักเก็บอิเล็กตรอน เพื่อให้เข้าใจความหมายของ parameters ทางฟิสิกส์ที่สำคัญของวงกักเก็บอิเล็กตรอน เนื่องจาก parameters เหล่านี้เกี่ยวข้องกับการบังคับลำอิเล็กตรอนในวงกักเก็บอิเล็กตรอน และเป็น parameters ที่เราต้องทำการวัด เพื่อให้รู้ว่าวงกักเก็บอิเล็กตรอนของเราอยู่ในสภาพที่ใกล้เคียงกับที่ออกแบบมาแค่ไหน และการเปรียบเทียบค่าของ parameters ที่วัดได้กับค่าที่ออกแบบ จะทำให้เรารู้ว่ามีอะไรผิดพลาดอยู่ในวงกักเก็บอิเล็กตรอน

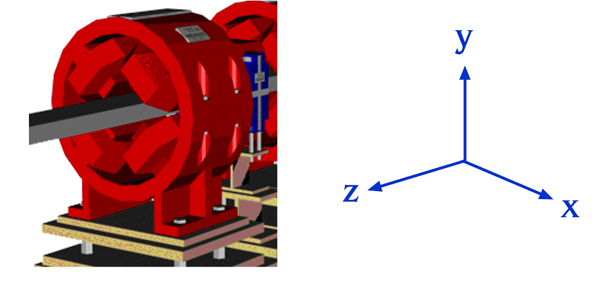
อิเล็กตรอนแต่ละตัวในลำอิเล็กตรอน เคลื่อนที่ภายใน vacuum chamber ของวงกักเก็บอิเล็กตรอนภายใต้อิทธิพลของสนามแม่เหล็กจากแม่เหล็กชนิดต่างๆ ที่ติดตั้งอยู่ในวงกักเก็บอิเล็กตรอน โดยที่วงกักเก็บอิเล็กตรอนของเครื่องกำเนิดแสงสยามมีแม่เหล็กชนิดต่างๆ คือ แม่เหล็กบังคับเลี้ยว (bending magnet) และแม่เหล็กสี่ขั้ว (quadrupole magnet) เรียงตัวกันในรูปแบบที่เรียกว่า Double Bend Acromat (DBA) จำนวนสี่ชุดต่อกันเป็นวง และยังมีแม่เหล็กชนิดอื่นๆ สำหรับการควบคุม parameter ต่างๆ ของลำอิเล็กตรอน

 

 

 

 

 

 

 

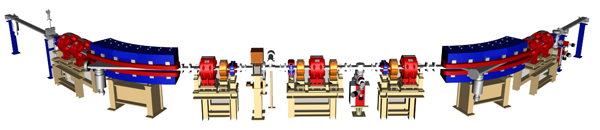   แสดงการเรียงแม่เหล็กแบบ DBA ประกอบเป็นหนึ่งในสี่ส่วนของวงกักเก็บอิเล็กตรอนของเครื่องกำเนิดแสงสยาม

           (สีน้ำเงินเป็น bending magnet สีส้มเป็น quadrupole magnet สีเหลืองเป็น sextupole magnet)

 

เราสามารถอธิบายการเคลื่อนที่ของอิเล็กตรอนภายใต้สนามแม่เหล็กเหล่านี้ได้ โดยการพิจารณาแรงที่กระทำต่ออิเล็กตรอนที่เคลื่อนที่ผ่านสนามแม่เหล็ก คือแรงลอเรนทซ์

1. Lorentz force

เมื่ออิเล็กตรอนซึ่งมีประจุเท่ากับ   เคลื่อนที่ด้วยความเร็ว  ผ่านสนามแม่เหล็ก  จะเกิดแรงลอเรนทซ์  กระทำต่ออิเล็กตรอน โดยที่

(1)     

ดังนั้น แรงลอเรนทซ์มีขนาดเท่ากับ  และมีทิศตั้งฉากกับทิศการเคลื่อนที่ของอิเล็กตรอนและตั้งฉากกับทิศของสนามแม่เหล็ก

 

2. การเคลื่อนที่ของอิเล็กตรอนผ่านส่วนต่างๆ ในวงกักเก็บอิเล็กตรอน

 

2.1 Drift space

Drift space  คือส่วน vacuum chamber ของวงกักเก็บอิเล็กตรอนที่ไม่มีแม่เหล็กอยู่ อิเล็กตรอนที่เคลื่อนที่ผ่านส่วนนี้จึงเคลื่อนที่เป็นเส้นตรง เนื่องจากไม่มีแรงลอเรนทซ์กระทำ

 

2.2 Bending magnet

 

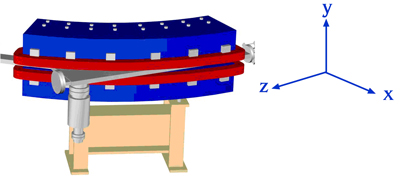
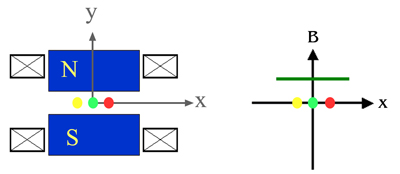
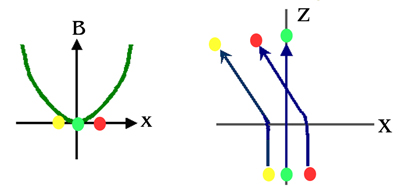
                        แสดงภาพ bending magnet อิเล็กตรอนเคลื่อนที่ในระนาบ x-z สนามแม่เหล็กอยู่ในทิศ -y

Bending magnet เป็นแม่เหล็กสองขั้ว โดยปกติจะมีขั้วเหนืออยู่ด้านบน และขั้วใต้อยู่ด้านล่าง bending magnet ในวงกักเก็บอิเล็กตรอนจึงสร้างสนามแม่เหล็กที่มีค่าคงที่ มีทิศชี้จากบนลงล่าง อิเล็กตรอนที่เคลื่อนที่ผ่าน bending magnet จะถูกผลักโดยแรงลอเรนทซ์ในทิศตั้งฉากกับการเคลื่อนที่และตั้งฉากกับทิศของสนามแม่เหล็ก ให้เคลื่อนที่เป็นส่วนโค้งของวงกลม ดังนั้น bending magnet ในวงกักเก็บอิเล็กตรอนจึงทำหน้าที่บังคับให้อิเล็กตรอนเลี้ยวโค้ง

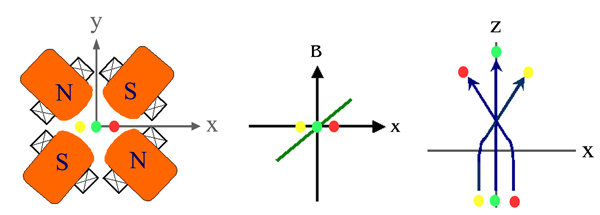
ภาพแรก แสดงภาคตัดขวางของ bending magnet วงกลมสีเหลือง เขียว แดง แทนอิเล็กตรอน N คือขั้วเหนือ S คือขั้วใต้ของสนามแม่เหล็ก กากบาทแสดงขดลวดไฟฟ้า

                                                  ภาพกลาง เส้นสีเขียวแสงค่าสนามแม่เหล็กในแนวแกน x

         ภาพขวาสุด แสดงเส้นทางการเคลื่อนที่ของอิเล็กตรอนในระนาบ x-z ภายใต้อิทธิพลของสนามแม่เหล็กของ bending magnet

โดยเราสามารถหาความสัมพันธ์ระหว่างค่าพลังงาน  ของอิเล็กตรอน ค่าสนามแม่เหล็ก  ของ bending magnet และ ค่ารัศมีความโค้ง  ของการเลี้ยวของอิเล็กตรอนได้จากความสัมพันธ์ระหว่างแรงลอเรนทซ์และแรงสู่ศูนย์กลาง โดยได้ความสัมพันธ์ คือ

(2)     

นั่นคือ หากเรานำเส้นทางการเคลื่อนที่ของอิเล็กตรอนภายใน bending magnet แต่ละตัวของวงกักเก็บอิเล็กตรอนมาต่อกัน เราจะได้วงกลมที่มีรัศมีเท่ากับ  เช่นอิเล็กตรอนในวงกักเก็บอิเล็กตรอนของเครื่องกำเนิดแสงสยาม มีพลังงาน E=1.2 GeV เลี้ยวโค้งใน bending magnet ซึ่งมีสนามแม่เหล็ก 1.44 เทสลา ด้วยรัศมีความโค้ง 2.78 เมตร

 

2.3 Quadrupole magnet

 

 

 

 

 

 

 

 

 

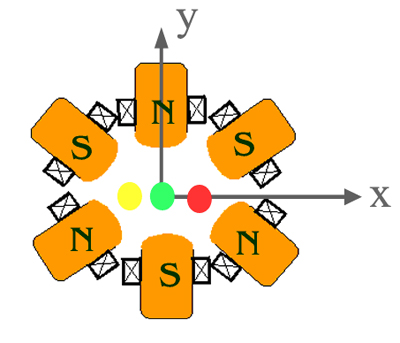
Quadrupole magnet เป็นแม่เหล็กสี่ขั้ว สร้างสนามแม่เหล็กที่มีค่าเปลี่ยนแปลงตามระยะห่างจากจุดศูนย์กลางของแม่เหล็ก ซึ่งก็คือจุดกลาง vacuum chamber สนามแม่เหล็กของ quadrupole จึงทำให้เกิดแรงลอเรนทซ์ที่มีขนาดเปลี่ยนแปลงตามระยะห่างของอิเล็กตรอนจากแกนกลางของ vacuum chamber ยิ่งอิเล็กตรอนอยู่ห่างจากจุดกลาง vacuum chamber มากเท่าไร จะยิ่งมีแรงลอเรนทซ์กระทำมากขึ้นเท่านั้น quadrupole จึงทำหน้าที่เหมือนเลนส์ที่โฟกัสลำอิเล็กตรอน

 

3. Beam dynamics

Beam dynamics หรือพลศาสตร์ของลำอนุภาค เป็นเรื่องที่ว่าด้วยการเคลื่อนที่ของลำอนุภาคในเครื่องเร่งอนุภาค หรือในวงกักเก็บอนุภาค ในที่นี้เราจะกล่าวถึง beam dynamics ของลำอิเล็กตรอนในวงกักเก็บอิเล็กตรอน

ในส่วนของ drift space ของวงกักเก็บอิเล็กตรอนซึ่งไม่มีแม่เหล็กอยู่ อิเล็กตรอนเคลื่อนที่เป็นเส้นตรงโดยไม่มีแรงใดๆ มากระทำ จึงไม่มีอะไรน่าสนใจ ในส่วนของ bending magnet ก็เช่นกัน อิเล็กตรอนที่เคลื่อนที่ผ่านสนามแม่เหล็กของ bending magnet เพียงถูกบังคับให้เลี้ยวโค้งเป็นส่วนของวงกลม ซึ่งก็ไม่มีอะไรน่าสนใจนัก ส่วนที่น่าสนใจคือผลของสนามแม่เหล็กของ quadrupole ต่อการเคลื่อนที่ของอิเล็กตรอนในวงกักเก็บอิเล็กตรอน

 

3.1 การโฟกัสลำอิเล็กตรอนโดย quadrupole

สนามแม่เหล็กของ quadrupole มีขนาดแปรผันตามระยะห่างจากศูนย์กลางแม่เหล็ก

 

 

 

 

 

 

 

 

 

 

 

เช่น จากรูป หากเราพิจารณาบนแกน  เราสามารถเขียนค่าสนามแม่เหล็ก  ของ quadrupole ได้คือ

(3)     

โดย  คือทิศของแกน  และ  เป็นค่าคงที่เรียกว่า gradient มีหน่วยเป็น เทสลาต่อเมตร ซึ่งคือค่าความชันของกราฟค่าสนามแม่เหล็กในรูป โดยค่าของ  ขึ้นอยู่กับ quadrupole แต่ละตัวและค่ากระแสไฟฟ้าที่ป้อนให้กับขดลวดรอบขั้วทั้งสี่ของ quadrupole

            หากเราแทนค่าสนามแม่เหล็กจากสมการ (3) ลงในสมการ (1) เราได้แรงลอเรนทซ์ ที่กระทำต่ออิเล็กตรอนในส่วนนี้ คือ

(4)     

โดย v เป็นความเร็วของอิเล็กตรอน ซึ่งจะเห็นว่าอิเล็กตรอนที่อยู่บนแกน  จะถูกผลักไปในทิศทาง   นั่นคือถูกผลักเข้าหาศูนย์กลางแม่เหล็กของ quadrupole

            เช่นเดียวกัน สนามแม่เหล็กบนแกน  คือ

(5)     

แรงลอเรนทซ์ในส่วนนี้ คือ

(6)     

ซึ่งจะเห็นว่าอิเล็กตรอนที่อยู่บนแกน  จะถูกผลักไปในทิศทาง   นั่นคือจะถูกผลักเข้าหาศูนย์กลางแม่เหล็กของ quadrupole เช่นกัน

            quadrupole magnet ดังในรูป 3.1 จึงทำหน้าที่ในการโฟกัสลำอิเล็กตรอนในแนวแกน x คล้ายกับการที่เลนส์นูนโฟกัสลำแสง โดยเราเรียก quadrupole magnet ที่โฟกัสลำอิเล็กตรอนในแนวแกน x นี้ว่า focusing quadrupole แต่หากเราหมุน quadrupole ในรูปไป 90 องศา หรือสลับขั้วเหนือและขั้วใต้เสีย เราจะได้ quadrupole ที่โฟกัสลำอิเล็กตรอนในแนวแกน y และเราเรียก quadrupole ชนิดนี้ว่า defocusing quadrupole

            จะเห็นว่า quadrupole แต่ละตัวนั้น สามารถจะโฟกัสลำอิเล็กตรอนในแนวแกนใดแกนหนึ่ง และ defocus ในอีกแกนหนึ่งเสมอ โดยเราไม่สามารถสร้าง quadrupole ที่โฟกัสในทั้งสองแกนพร้อมกันได้ นั่นคือ focusing quadrupole ทำหน้าที่เเหมือนเลนส์นูนในแนวแกน x แต่เป็นเลนส์เว้าในแนวแกน y และเป็นในทางตรงกันข้ามสำหรับ defocusing quadrupole

 

 

 

 

 

 

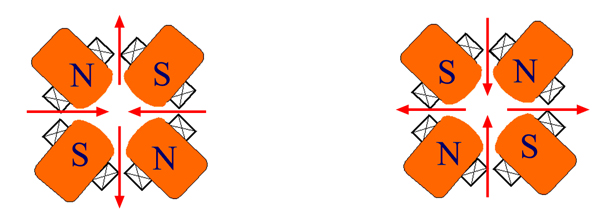       focusing quadrupole และ defocusing quadrupole

            อย่างไรก็ตาม เราสามารถทำการโฟกัสลำอิเล็กตรอนในทั้งสองแกนได้ โดยการนำ quadrupole ทั้งสองชนิดมาวางต่อกัน ซึ่งจะทำให้ได้ focusing เฉลี่ยในทั้งสองแกน คล้ายกับการนำเลนส์นูนและเลนส์เว้ามาวางต่อกัน

 

3.2 Ideal orbit

            เรานิยาม ideal orbit เป็นเส้นทางการเคลื่อนที่ของอิเล็กตรอนที่ผ่านศูนย์กลางของ quadrupole ทุกตัว นั่นคือ หากการ alignment ของแม่เหล็กทุกตัวสมบูรณ์แบบ ไม่มีความคลาดเคลื่อนเลย ideal orbit ของเราจะอยู่กลาง vacuum chamber ของวงกักเก็บอิเล็กตรอน และหากเราบรรจุอิเล็กตรอนเพียง 1 ตัวให้เคลื่อนที่อยู่บน ideal orbit อิเล็กตรอนจะเคลื่อนที่โดยไม่มีการส่าย เนื่องจากสนามแม่เหล็กที่ศูนย์กลาง quadrupole เป็นศูนย์ จึงไม่มีแรงกระทำต่ออิเล็กตรอน ยกเว้นเมื่อมันเลี้ยวโค้งใน bending magnet เท่านั้น

            อย่างไรก็ตาม เรากักเก็บอิเล็กตรอนจำนวนมากไว้ในวงกักเก็บอิเล็กตรอน เราไม่มีทางวางอิเล็กตรอนทุกตัวลงบน ideal orbit ได้ หรือถึงแม้เราทำได้ อิเล็กตรอนก็ผลักกันเนื่องจากแรงผลักทางไฟฟ้า อิเล็กตรอนส่วนใหญ่ในวงกักเก็บอิเล็กตรอนจึงไม่อยู่บน ideal orbit  แต่จะส่ายไปรอบ ideal orbit เนื่องมาจากผลของการ focus และ defocus ของ quadrupole

            เรานิยามระบบแกนอ้างอิงของอิเล็กตรอนในวงกักเก็บอิเล็กตรอนด้วยแกน 3 แกน คือ (x,y,s) ดังรูป

 

 

 

 

 

 

 

 

 

 

 

 

โดย x และ y ตั้งฉากกับกับ ideal orbit เสมอ และ ทิศทางของ s หมุนไปตาม ideal orbit ดังนั้นแกน s ในวงกักเก็บอิเล็กตรอนจึงทำหน้าที่เป็นแกนเวลา t โดยหากอิเล็กตรอนเคลื่อนที่ด้วยความเร็ว v เราได้  ดังนั้น

(7)       

 

3.3 Betatron oscillation

จากนิยามของแรง เราได้

โดย p เป็นโมเมนตัม m เป็นมวลอิเล็กตรอน  เรียกว่า relativistic factor (มีค่าเท่ากับพลังงานอิเล็กตรอนหารด้วยพลังงานมวลนิ่ง mc² ของอิเล็กตรอน) และจากสมการของ Lorentz force ของอิเล็กตรอนที่เคลื่อนที่ผ่านสนามแม่เหล็กของ quadrupole เราได้

หรือเราเขียนสมการใหม่ได้เป็น

(8)       

โดยที่  เป็นค่า quadrupole strength มีหน่วยเป็น m^-2

            สมการ (8) เป็นรูปเดียวกับสมการการเคลื่อนที่ของวัตถุที่ติดอยู่บนปลายสปริงที่มีค่า spring constant เท่ากับ  ดังนั้น เราเห็นได้ว่าอิเล็กตรอนที่เคลื่อนที่ผ่านสนามแม่เหล็กของ quadrupole จะเคลื่อนที่แบบสั่นในแนวแกน x และหากเราวาดตำแหน่งของอิเล็กตรอนในแนวแกน x ไปตามแนวของวงกักเก็บอิเล็กตรอน เราจะได้เส้นทางการเคลื่อนที่ที่ส่ายไปมาเป็นรูปคลื่น เหมือนกับอิเล็กตรอนติดอยู่บนปลายสปริงที่ยืดหดในแนวแกน x โดยมีตำแหน่ง equilibrium อยู่บน ideal orbit และสปริงนั้นเคลื่อนที่ไปตาม ideal orbit แตกต่างกันตรงที่ค่า k ในกรณีนี้ไม่ใช่ค่าคงที่ แต่เปลี่ยนแปลงไปตามตำแหน่งต่างๆ ในวงกักเก็บอิเล็กตรอน เช่น เมื่อผ่าน drift space ค่า k กลายเป็นศูนย์และอิเล็กตรอนเคลื่อนที่เป็นเส้นตรง และการเคลื่อนที่ในแนวแกน y ก็เป็นลักษณะเดียวกัน

 

 

 

 

 

 

 

 

 

 

 

 

แสดง betatron oscillation การเปรียบเทียบเหมือนอิเล็กตรอน (วงกลมสีแดง) ติดอยู่ปลายสปริงซึ่งสั่นขึ้นลงพร้อมกับเคลื่อนที่ไปตาม ideal orbit (เส้นทึบรูปแปดเหลี่ยม) รอบวงกักเก็บอิเล็กตรอน

การเคลื่อนที่ส่ายไปมาในแนวแกน x และ y ของอิเล็กตรอนนี้เราเรียกว่า betatron oscillation โดยจำนวนลูกคลื่นของการส่ายต่อหนึ่งรอบวงกักเก็บอิเล็กตรอนเรียกว่า betatron tune โดยใช้สัญลักษณ์ และ  เช่น หาก   หมายความว่าอิเล็กตรอนจะส่ายในแนวแกน x เป็นจำนวน 4 กับอีก ¾ ลูกคลื่นจึงกลับมาที่เดิม

Betatron tune นี้มีความสำคัญกับความสถียร (stability) ของลำอิเล็กตรอนในวงกักเก็บอิเล็กตรอน โดยหาก  หรือ   มีค่าเป็นจำนวนเต็ม หรือครึ่งหนึ่งของจำนวนเต็ม จะทำให้เกิด resonance อันดับที่หนึ่งและสอง (ตามลำดับ) ของ betatron oscillation และอิเล็กตรอนจะส่ายด้วย amplitude ที่สูงมากจนชนกับผนังของ vacuum chamber และหายไป (เกิด beam loss) หรือหาก  หรือ   มีค่าเป็น 1/3 ของจำนวนเต็ม จะเป็น resonance อันดับที่สาม ซึ่ง resonance อันดับสามนี้มีความสัมพันธ์กับสนามแม่เหล็กของ sextupole magnet ซึ่งในกรณีที่เราใช้ sextupole magnet ในการแก้ chromaticity อาจทำให้เกิด beam loss หาก betatron tune อยู่ใกล้ resonance อันดับที่สาม

 

3.4 Phase space และ Phase ellipse

จากสมการ (8) เราสามารถแก้สมการหา solution เพื่อบอกตำแหน่งของอิเล็กตรอนที่จุดต่างๆ ของวงกักเก็บอิเล็กตรอนได้ ซึ่ง Solution ของสมการ (8) มีรูปเดียวกับในกรณีของสปริง คือ

(9)     

โดย  เป็น amplitude ของการส่าย และ  เรียกว่า betatron phase ในการบอกพิกัดของอิเล็กตรอนนั้น นอกจากบอกตำแหน่ง x แล้ว เราต้องบอกมุมของการเคลื่อนที่ด้วย คือ  ซึ่งคือมุมการเคลื่อนที่ของอิเล็กตรอนที่ทำกับ ideal orbit  โดยเราเรียกระบบพิกัด  นี้ว่า  phase space หากเราวางพิกัดของอิเล็กตรอนแต่ละตัวในลำอิเล็กตรอนที่จุดใดจุดหนึ่งของวงกักเก็บอิเล็กตรอน ลงใน phase space   เราจะได้รูปวงรีใน phase space ซึ่งบรรจุอิเล็กตรอนทั้งหมดไว้ เราเรียกวงรีนี้ว่า phase ellipse

            ความสำคัญของ phase ellipse อยู่ที่ทฤษฎีที่เรียกว่า Liouville’s Theorem ซึ่งกล่าวว่า พื้นที่ของ phase ellipse มีค่าคงที่เสมอในทุกๆ จุดในแนวการเคลื่อนที่ของลำอิเล็กตรอน ซึ่งทฤษฎีนี้ทำให้เราสามารถทำนายตำแหน่งของอิเล็กตรอนที่จุดใดๆ ในวงกักเก็บอิเล็กตรอนได้ หากเรารู้ตำแหน่งที่จุดใดจุดหนึ่ง

            ขณะที่ลำอิเล็กตรอนเคลื่อนที่ไปในวงกักเก็บอิเล็กตรอน phase ellipse จะเปลี่ยนรูปร่างไป (แต่ยังเป็นวงรี) แต่พื้นที่ของวงรียังคงที่เสมอ รูปร่างของวงรีของ phase ellipse นี้สัมพันธ์กับตัวแปรที่เรียกว่า betatron functions

           

3.5 Betatron functions

Betatron functions เป็น parameter ที่เป็นตัวบอกรูปร่างของ phase ellipse ในแต่ละจุดของเส้นทางการเคลื่อนที่ของลำอิเล็กตรอน โดยในทางคณิตศาสตร์ เราสามารถเขียนสมการสำหรับรูปวงรีใดๆ ในพิกัด   ได้คือ

(10)      

ซึ่งเป็นรูปวงรีที่มีพื้นที่เท่ากับ  และมีจุดตัดแกน  และแกน  ดังในรูป

 

 

 

 

 

 

 

 

 

 

 

 

 

 

เราเรียก parameters 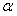,  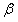และ  ว่า betatron functions ซึ่งเป็น parameters ที่บอกลักษณะการเคลื่อนที่ของลำอิเล็กตรอนภายในวงกักเก็บอิเล็กตรอน และเราเรียก  ว่า beam emittance ซึ่งมีค่าคงที่เฉพาะสำหรับวงกักเก็บอิเล็กตรอนแต่ละวง

ตัวอย่างที่ง่ายที่สุดของการเปลี่ยนแปลงรูปร่างของ phase ellipse คือกรณีที่ลำอิเล็กตรอนเคลื่อนที่ไปตาม drift space เนื่องจากไม่มีสนามแม่เหล็กจึงไม่มี Lorentz force กระทำต่ออิเล็กตรอน ดังนั้นมุมการเคลื่อนที่ของอิเล็กตรอนในแนวแกน   คงที่ตลอดระยะของ drift space ในขณะที่ตำแหน่งในแนวแกน  เปลี่ยนแปลงไป แต่อย่างไรก็ตาม พื้นที่ของวงรียังคงที่เสมอ นั่นคือค่า  คงที่ แต่ betatron functions 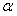,  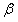และ  เปลี่ยนไป

การเปลี่ยนแปลงของ phase ellipse ของอิเล็กตรอนที่เคลื่อนที่ใน drift space

หากเราแทนค่า solution ในสมการ (9) ลงในสมการวงรีของ phase ellipse (10) เราได้ amplitude ของ betatron oscillation คือ  และดังนั้นเราได้ solution สำหรับตํแหน่งในแนวแกน x ของอิเล็กตรอนในวงกักเก็บอิเล็กตรอน คือ

(11)      

จะเห็นว่าอิเล็กตรอนในวงกักเก็บอิเล็กตรอนจะอยู่ที่ตำแหน่งระหว่าง  โดยที่ค่า  นี้สัมพันธ์กับ beam size คือขนาดของลำอิเล็กตรอน ดังนั้นเราสามารถกำหนดขนาดของลำอิเล็กตรอนที่จุดใดๆ ในวงกักเก็บอิเล็กตรอนได้โดยการเปลี่ยนค่า betatron functions ซึ่งทำได้โดยการเปลี่ยนค่าสนามแม่เหล็กของ quadrupoles

 

3.6 Dispersion function

ที่เราพิจารณาทั้งหมดข้างบนนั้น เป็นการพิจารณาการเคลื่อนที่ของอิเล็กตรอนที่มีพลังงานค่าหนึ่ง แต่ในความเป็นจริง อิเล็กตรอนในวงกักเก็บอิเล็กตรอนไม่ได้มีพลังงานเท่ากันทั้งหมด และเนื่องจากพลังงานของอิเล็กตรอนเป็นตัวกำหนดขนาดของรัศมีความโค้งเมื่อเคลื่อนที่ผ่าน bending magnet เช่น จากสมการ (2) เราเห็นว่าอิเล็กตรอนที่มีพลังงานสูงกว่าจะมีค่ารัศมีความโค้งมากกว่า นั่นคือจะเคลื่อนที่เป็นวงที่กว้างกว่าอิเล็กตรอนที่พลังง่านต่ำกว่า และเนื่องจากส่วนโค้งของการเคลื่อนที่นี้เป็นส่วนหนึ่งของ ideal orbit ดังนั้นอิเล็กตรอนแต่ละตัวซึ่งมีพลังงานแต่ละค่าก็จะมี ideal orbit เป็นของตัวเอง และเมื่อเคลื่อนที่ผ่านสนามของ quadrupole ก็จะเกิด betatron oscillation รอบ ideal orbit ของตัวเอง

 

 

 

 

 

 

 

 

 

 

หากเรากำหนดให้  เป็นพลังงานของอิเล็กตรอนที่ออกแบบไว้สำหรับวงกักเก็บอิเล็กตรอน (= 1.2 GeV สำหรับเครื่องกำเนิดแสงสยาม) เราจะได้ว่าอิเล็กตรอนที่มีพลังงาน  จะมี ideal orbit ที่ขยับไปเป็นค่าแปรผันกับค่า  นั่นคือ อิเล็กตรอนนี้จะมี ideal orbit ใหม่อยู่ที่

โดยที่  มีค่าเปลี่ยนไปตามตำแหน่งของวงกักเก็บอิเล็กตรอน เราเรียก  ว่า dispersion function และเมื่อรวมผลของ betatron oscillation จากสมการ (11) เราสามารถเขียนตำแหน่งของอิเล็กตรอนในแนวแกน x ได้คือ

(12)      

โดยเทอมแรกเป็น ideal orbit ใหม่ของอิเล็กตรอนที่มีพลังงาน  และเทอมที่สองเป็น betatron oscillation รอบ ideal orbit นั้น

            ในแนวแกน y นั้น dispersion function ควรจะมีค่าเป็นศูนย์ เนื่องจาก bending magnet ของวงกักเก็บอิเล็กตรอนนั้นส่งผลต่อการเคลื่อนที่ในแนวแกน x เท่านั้นความแตกต่างของพลังงานของอิเล็กตรอนจึงไม่ทำให้เกิดการเลื่อนของ ideal orbit ในแนวแกน y  นอกเสียจากในกรณีที่คุณภาพของแม่เหล็ก หรือการ alignment ของแม่เหล็กไม่ดี ทำให้มีสนาม bending magnet ในแนวราบ

 

3.7 Momentum compaction factor

Parameter อีกตัวหนึ่งที่เกี่ยวข้องกับการที่อิเล็กตรอนในวงกักเก็บอิเล็กตรอนมีพลังงานต่างกัน คือ momentum compaction factor โดยเป็นตัวบอกความสัมพันธ์ระหว่างการเปลี่ยนแปลงของระยะการเคลื่อนที่ของอิเล็กตรอน (path length) กับค่าพลังงาน  โดยหาก L₀ เป็นค่า path length ของอิเล็กตรอนที่มีพลังงานเท่ากับ designed energy E₀ (นั่นคือ L₀ เป็นความยาวรอบวงกักเก็บอิเล็กตรอนของ ideal orbit ของอิเล็กตรอนพลังงาน E₀ ) และ  เป็นค่า path length ที่เปลี่ยนไปเมื่ออิเล็กตรอนมีพลังงานเปลี่ยนไป  เรานิยาม momentum compaction factor คือ

(13)     

และเราได้ความสัมพันธ์ระหว่าง momentum compaction factor กับ dispersion function คือ

(14)      

โดยเครื่องหมาย  หมายถึงค่าเฉลี่ยรอบวงกักเก็บอิเล็กตรอน และ  เป็นค่ารัศมีความโค้งของอิเล็กตรอน

 

3.8 Synchrotron oscillation

Betatron oscillation นั้นเป็นการเคลื่อนที่แบบสั่นของอิเล็กตรอนในแนวตั้งฉากกับการเคลื่อนที่ คือในแนวแกน x และ y แต่นอกจากการสั่นในแนวตั้งฉากแล้ว อิเล็กตรอนในวงกักเก็บอิเล็กตรอนยังมีการสั่นในแนวของการเคลื่อนที่ด้วย คือสั่นในแนวแกน s เราเรียกการสั่นในแนวของการเคลื่อนที่นี้ว่า synchrotron oscillation

ในการชดเชยพลังงานให้อิเล็กตรอนโดย RF cavity นั้น สนามไฟฟ้าใน RF cavity มี phase ที่ถูกออกแบบไว้ค่าหนึ่ง เรียกว่า synchronous phase โดยอิเล็กตรอนควรจะมาถึง RF cavity เมื่อ phase ของอิเล็กตรอนมีค่าเท่ากับ synchronous phase พอดี แต่เนื่องจากในความเป็นจริงแล้วอิเล็กตรอนส่วนใหญ่จะมาถึง RF cavity ที่ phase แตกต่างจาก synchronous phase เล็กน้อย ดังนั้นเมื่อถูกเร่งโดยสนามไฟฟ้าของ RF cavity แล้ว phase ของอิเล็กตรอนเหล่านั้นจะมีค่าเปลี่ยนแปลงขึ้นลงรอบ synchronous phase การสั่นของ phase นี้ทำให้อิเล็กตรอนเคลื่อนที่แบบสั่นในแนวของการเคลื่อนที่ คือแนวแกน s เราเรียกการสั่นในแนวเดียวกับการเคลื่อนที่นี้ว่า phase oscillation หรือ synchrotron oscillation และจำนวนลูกคลื่นของการสั่นต่อหนึ่งรอบวงกักเก็บอิเล็กตรอนในกรณีนี้ เราเรียกว่า synchrotron tune โดยใช้สัญลักษณ์  คล้ายกับในกรณีของ betatron oscillation

 

3.9 Chromaticity

เรารู้ในกรณีการโฟกัสแสงของเลนส์นูนว่า แสงที่พลังงานไม่เท่ากันจะถูกโฟกัสไปที่จุดต่างกัน ในกรณีการโฟกัสลำอิเล็กตรอนด้วย quadrupole ในวงกักเก็บอิเล็กตรอนก็เป็นเช่นเดียวกัน คืออิเล็กตรอนที่มีพลังงานต่างกันจะถูกโฟกัสด้วย quadrupole ต่างกัน เราเรียกปรากฏการณ์นี้ว่า chromatic aberration โดยหากเราเปรียบเทียบ focusing quadrupole เป็นเลนส์นูน เราจะได้การโฟกัสลำอิเล็กตรอนดังรูป

 

 

 

 

 

 

 

 

 

เนื่องจากการโฟกัสลำอิเล็กตรอนที่ต่างกัน ทำให้ betatron oscillation ของอิเล็กตรอนที่พลังงานไม่เท่ากัน มีความแตกต่างกัน ซึ่งส่งผลทำให้ betatron tune มีค่าไม่เท่ากันด้วย ดังนั้น betatron tune จึงเปลี่ยนไปเมื่อพลังงานของอิเล็กตรอนเปลี่ยนไป นั่นคือ ค่า tune ที่เปลี่ยนไปนั้นแปรผันโดยตรงกับค่า  หรือเขียนเป็นสมการได้ คือ

(15)     

โดยเราเรียก  ว่า chromaticity

            เราสามารถชดเชย chromaticity นี้ได้โดยการติดตั้งแม่เหล็กหกขั้ว หรือ sextupole magnet ในวงกักเก็บอิเล็กตรอน

 

3.10 Sextupole magnet

Sextupole magnet เป็นแม่เหล็กหกขั้ว ให้สนามแม่เหล็กที่มีค่าเพิ่มขึ้นเป็นพาราโบลาตามระยะห่างจากจุดศูนย์กลางแม่เหล็ก

 

 

 

 

 

 

 

 

คุณสมบัติที่สำคัญของสนามแม่เหล็กของ sextupole คือ จะ focus อิเล็กตรอนที่มีพลังงานสูง และ defocus อิเล็กตรอนที่พลังงานต่ำ นั่นคือ sextupole ทำหน้าที่เป็นเลนส์นูนสำหรับอิเล็กตรอนพลังงานสูง และเป็นเลนส์เว้าสำหรับอิเล็กตรอนพลังงานต่ำ ทำให้อิเล็กตรอนพลังงานต่างกันถูกโฟกัสไปยังจุดเดียวกัน

 

 

 

 

 

 

 

 

 

 

4. Transfer matrices

ในการคำนวณตำแหน่งและมุมของอิเล็กตรอนในวงกักเก็บอิเล็กตรอน เราสามารถแทนส่วนต่างๆ ของ วงกักเก็บอิเล็กตรอนด้วย matrix ทางคณิตศาสตร์

 

4.1 Drift space matrix

ตัวอย่างเช่นอิเล็กตรอนที่เคลื่อนที่ผ่าน drift space ซึ่งเคลื่อนที่เป็นเส้นตรง หากอิเล็กตรอนเริ่มต้นที่ตำแหน่งและมุม  ผ่าน drift space ความยาว L

เราได้ว่าที่ปลาย drift space นั้นอิเล็กตรอนจะอยู่ที่ตำแหน่ง  คือ

ซึ่งเราเขียนสองสมการนี้ในรูปของ matrix ได้ คือ

           

ดังนั้นเราสามารถแทน drift space ความยาว  ในวงกักเก็บอิเล็กตรอนได้ด้วย drift space matrix คือ

(16)      

 

4.2 Thin lense quadrupole

ก่อนอื่น เราพิจารณาการโฟกัสอิเล็กตรอนโดย focusing quadrupole ที่ทำหน้าที่เหมือนเลนส์นูนบาง (quadrupole ที่สมมติว่ามีความหนาน้อยมากเมื่อเทียบกับความยาวโฟกัส) ที่มีค่าความยาวโฟกัสเท่ากับ f และอิเล็กตรอนเริ่มต้นที่ตำแหน่ง   และ  (ขนานกับ ideal orbit) ดังรูป

 

 

 

 

 

 

 

 

 

เราได้ค่ามุมที่เปลี่ยนไปจากการโฟกัสของเลนส์ (สมมติ x มีค่าน้อยเมื่อเทียบกับ f  ) คือ

           

ดังนั้นเราได้ตำแหน่งอิเล็กตรอนเมื่อเพิ่งออกจากเลนส์ คือ

หรือเขียนเป็นสมการ matrix ได้คือ

           

โดยสำหรับ thin lense quadrupole นี้ เราได้ค่าความยาวโฟกัสสัมพันธ์กับค่า quadrupole strength k และความหนา l คือ f=1/kl ดังนั้นเราได้ thin lense focusing quadrupole matrix คือ

(17)      

และคล้ายๆ กันสำหรับ defocusing quadrupole เพียงแต่เราต้องกลับเครื่องหมายของการโฟกัส (เนื่องจากการ defocus หรือเลนส์เว้านั้นทำให้มุมเพิ่มขึ้น) นั่นคือเราได้ thin lense defocusing quadrupole matrix คือ

(18)             

โดยที่ค่า k สำหรับ QF มีเครื่องหมายเป็นบวก แต่ สำหรับ QD มีเครื่องหมายเป็นลบ

 

4.3 การโฟกัสลำอิเล็กตรอนด้วยคู่ QF และ QD

จาก transfer matrix ของ thin lense quadrupole ข้างบน เราสามารถแสดงได้ว่าเราสามารถโฟกัสลำอิเล็กตรอนในทั้งสองแกนพร้อมกันได้โดยการนำ QF และ QD มาวางต่อกัน เช่น หากเรานำ QD และ QF ที่มี quadrupole strength เท่ากันมาวางต่อกัน โดยมีระยะห่าง L เราได้ transfer matrix รวม คือ (อิเล็กตรอนผ่าน QD ผ่าน drift space แล้วผ่าน QF)

ซึ่งเป็น transfer matrix ที่เป็น focusing มีค่าความยาวโฟกัส f²/L

 

4.4 Quadrupole matrix และ bending matrix

ในกรณีปกติทั่วไป สำหรับ quadrupole matrix ที่ไม่ใช่ thin lense คือมีความหนาพอสมควร เราได้ transfer matrix  คือ

 

สำหรับ QF

(19)     

 

สำหรับ QD

(20)     

 

และสำหรับ bending magnet เราได้ bending transfer matrix คือ

(21)      

โดย  เป็น deflection angle ของ bending magnet และ  เป็นรัศมีความโค้ง

 

โดย

ดร.ศุภกร รักใหม่

สถาบันวิจัยแสงซินโครตรอน (องค์การมหาชน)